カリウム-アルゴン法

カリウム-アルゴン法（カリウム-アルゴンほう）は、カリウム40(⁴⁰K)の放射性崩壊を利用した放射年代測定法の一種。

概要

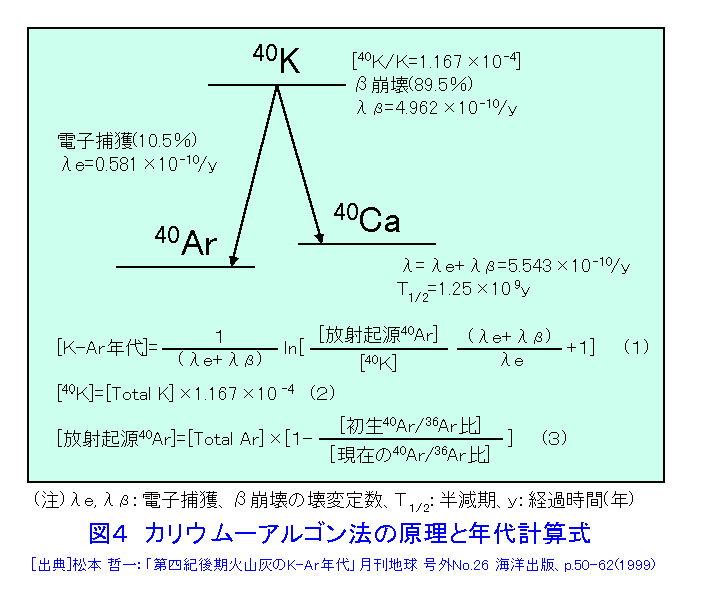
1955年に登場した手法で、マグマに含まれている放射性元素「カリウム40」(⁴⁰K)は、約13億年の半減期で放射性崩壊して約89%が「カルシウム40」(⁴⁰Ca)に約11%が「アルゴン40」(⁴⁰Ar)という別の元素に変わる。

カリウム40の崩壊

• ${\displaystyle {\ce {{}^{40}K{} {\mathit {e}}^{-}->{}^{40}Ar\ \gamma }}}$${\displaystyle {\rm {(1,505MeV)}}}$ , ${\displaystyle {\rm {\lambda \varepsilon =0,581\cdot 10_{-10}an_{-1}}}}$

• ${\displaystyle {\ce {{}^{40}{K}-> {}^{40}Ca\ \beta^-}}}$ ${\displaystyle {\rm {\mbox{(1,311 MeV)}}}}$ , ${\displaystyle {\rm {\lambda \varepsilon =4,962.10_{-10}an_{-1}}}}$

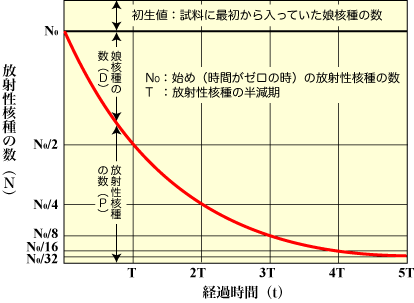
こうした変化はマグマの中で常に起きているが、ガスである「アルゴン40」はマグマから抜け出してしまう。しかし火山の噴火などによって地表に出たマグマは冷えて固まる。そうすると「アルゴン40」は岩石の中に閉じ込められ、時間とともにその量を増していく。放射壊変による「カリウム40」の減少のしかた（あるいは「アルゴン40」の増加のしかた）は方程式であらわされている。

• 方程式

${\displaystyle t={\frac {t_{\frac {1}{2}}}{\ln(2)}}\ln \left({\frac {K_{f} {\frac {Ar_{f}}{0.109}}}{K_{f}}}\right)}$

この方程式を積分することによって、マグマが結晶化した時点から現在までの時間にどれだけ「アルゴン40」が増えたかが予測される。これと観測された「アルゴン40」の量とを比べれば、マグマが固化してから現在までの経過時間がわかる。

誤差

大気中アルゴンの混入や試料の変質により、実年代と見かけ上の年代に誤差が生じる。例えば試料が長石類の場合、炭酸塩化、絹雲母化、粘土化などの弱い熱水変質を受けるとカリウムが減少し、実際の年代より古い年代が導き出されることがある。

この欠点を持つカリウム-アルゴン法に代わり、アルゴン - アルゴン法が開発された。

参考文献

• 『ゼロと無限の科学』(ニュートンムック)ニュートンプレス 2006年2月 ISBN 4315517690

脚注

関連項目

• 放射年代測定

外部リンク

• 内海茂、柴田賢、K-Ar 年代測定における誤差について (PDF) 『地質調査所月報』 Vol.31 No.6 (1980)
• 松本哲一, 宇都浩三, 柴田賢、歴史溶岩のアルゴン同位体比 ―若い火山岩のK-Ar年代測定における初生値補正の重要性― 『Journal of the Mass Spectrometry Society of Japan.』 1989年 37巻 6号 p.353-363, doi:10.5702/massspec.37.353
• 佐藤佳子, 熊谷英憲, 田村肇, 川畑博、レーザー融解 K-Ar 法による極微量年代測定法の開発 『地球化学』 2008年 42巻 4号 p.179-199, doi:10.14934/chikyukagaku.42.179